FuRSST Logo
 Future Reservoir Simulation Systems and Technology Research
Research Team Resources Industry Recruiting  
Software Research
 Solvers Research
 Advanced Process Research

With growing physical complexity, the importance of nonlinear and linear solution processes is underscored. Our aim is to make fundamental advances in several challenge areas that arise ubiquitously in complex application scenarios. Leveraging these fundamental advances, we also aim to develop lasting, general, and robust solution technologies and methods. Our ultimate measure of success will be the wide and successful adoption of our methods in industrial and academic simulators to perform full-resolution, full-Physics modeling of seriously complex large-scale emerging processes.

Spatiotemporal Locality
 Asymptotic Nonlinear Convergence
 Implicit Solvers with Embedded Timestep & Error Control
 Nonlinear Coupling of Multiphysics

Spatiotemporal Locality

Locality is inherent to all transient flow and transport phenomena. The superposition of the two disparate spatiotemporal characteristic scales that underly flow and transport leads to a problem of dimensionality. While the extent of an adequate simulation domain is dictated by the nature of flow, the resolution of its discrete form is restricted by the transport variables.

As a first response to this issue of dimensionality, Adaptive Discretization methods have been devised to exploit an a priori understanding of locality in order to reduce the computational cost of simulations. While such methods have provided various degrees of success in applications, it remains that they are inherently restricted by the fidelity of the discretization under aggressive adaptivity.

Our work in this areas seeks an alternate strategy. We are devising nonlinear solution processes that internally adapt the level of computation to precisely match that of the underlying spatiotemporal changes in state. This will enable the efficient use of high-fidelity, static, and full-resolution discretizations that do not require global computations unless absolutely necessary.

Fundamental Question: Over a Newton iteration, which cells will experience a nonzero update in state?

Encouraged by an initial result, we are answering this question for general flow and transport, independent of the spatial discretization that is used. The result is obtained by the application of the infinite dimensional Newton iteration process to the semidiscrete governing equations. That is, suppose that the governing equation has the form,

Then the semidiscrete fully-implicit form is simply,

In reservoir simulation, the generally nonlinear and heterogeneous flow term is discretized in space using an accurate method. We will not perform this discretization. rather we will work with the infinite dimensional (continuous) problem itself.

Over a single time-step, the initial state is,

and the subsequent state at the end of the time-step is,

Newton's method can be applied to any differentiable nonlinear operator, including an infinite dimensional form. The iteration produces the sequence of iterations,


Note that this is a sequence of functions defined over the entire domain. The equation for the updates can be written as,

where the generalized Frechet derivative of the infinite dimensional residual equation is a linear partial differential equation. The Newton updates in a reservoir simulator are numerical approximations to the infinite dimensional update that can be obtained analytically in certain cases.

We have derived sharp conservative estimates for the analytical infinite dimensional Newton updates for general sequential flow and transport!

Using these estimates which are essentially free to evaluate, we can tell which cells within the domain will experience change over a Newton step, and which ones will not. A whitepaper describing this process is available here.

Our current research in this area is focused on:
  1. Deriving estimates for the coupled form of reactive flow and transport in multiple dimensions.
  2. Extensions to general nonlinear multicomponent advection, diffusion, and reaction problems including thermal.
  3. Exploration of applications in fractured and stimulated media.
Application 1: solvers that only solve for cells that will experience change.

In any iterative nonlinear solution process that generates iterates that are the solution of a large sparse linear system, why solve for the entire system if we know that only a portion of the resulting vector has nonzero entries? Moreover, at initial iterates, far from the solution, it may be unnecessary to compute the linear solution very accurately. Our universal results on locality, provide an a priori identification of these vector components that is available at negligible cost. We are developing application grade solvers that do this. Compared to detection methods that are designed at the discrete level such as in this article, our methods are general to both flow and transport, and are available by evaluating a single formula!

Our current research in this area is focused on:
  1. Devising solvers that do not degrade the convergence rate of the nonlinear iteration.
  2. Developing strategies that adaptively alter the target linear convergence tolerance.
Application 2: Adaptive Mesh Refinement inside the nonlinear solver and not within the discretization.

Particularly in the case of fast physics such as flow, the nonlinear iteration updates may have relatively global support. In cases where these updates decay rapidly around certain points and very slowly near the boundaries, it is desirable to use adaptively localized meshes. Keeping the discretization mesh static, we are devising methods that solve the nonlinear residual using adaptive solver meshes. These ideas are inspired by nonlinear control optimization methods that adapt the resolution of control variables to reduce computational costs.

Application 3: Multirate nonlinear methods

Newton's method is an explicit Euler discretization of the Newton Flow system of Ordinary Differential Equations using a stepsize of one. We propose to develop multirate or local timestepping methods to integrate the Newton Flow system. Using our results on spatiotemporal locality, we can decompose the spatial domain into several sets based on the anticipated rate of change in state.
Asymptotic Nonlinear Convergence

Safeguarding tactics are readily used to make Newton's Method robust. That is, a safeguarded method is one that will ultimately converge to the answer if only it is given a chance to do so. This research direction builds upon recent advances in safeguarding to address the next question in the evolution of our understanding of converge.

Fundamental Question: How long will it take for a (safeguarded) Newton iteration to converge?

Our study on spatiotemporal locality is revealing. Newton updates for flow decay rapidly in the vicinity of nonzero entries in the residual. Away from such points, the decay is slow. The precise character of this decay depends on compressibility, time, and mobility. Newton updates for transport behave differently. The decay depends on an exponential ratio that is a nonlinear function of wave speeds.

Over one time-step, the number of iterations required for convergence is at least equal to the number of iterations required for the spatial support of non-zeros entries in the updates to encompass the number of cells that change over the time-step. We are deriving theoretical characterizations of this limit in terms of the decay parameters that have been derived to characterize locality.

This research will ultimately lead to an analogous result to the Courant-Friedrichs-Lewy condition for explicit time-step stability that is applicable to assessing the convergence rate of an implicit time-step using a safeguarded Newton iteration.

Since our results on locality are independent of the spatial discretization, it is conjectured that the convergence rate fo Newton is also independent of discretization. Rather, the important factors relate solely to the physics.

Application 1: Is it possible to somehow accelerate the nonlinear convergence rate of a safeguarded method?

Research is underway to develop nonlinear iterations that have an expanded spatiotemporal support. Our initial point of departure is to seek methods that are motivated by higher-order ODE integration. While expanded support has been observed with such methods, the additional computational costs of each step render them value-neutral. Current research is focused on retaining the expanded support properties while reducing the computational cost per iteration. Our approach to achieving this uses a differential geometry perspective, where the dynamics of motion can be abstracted with linear transformation operators. A promising idea is to develop extrapolation approaches on the Frenet Frame of the solution path.

Application 2: If we have bounds on the asymptotic convergence rates, we may better control timestep size selection for convergence.
A direct application of our results that characterize convergence rate is to use them in order to select timestep size in a manner that minimizes the computational cost per unit time advancement in implicit simulation. Suppose that at a specific timestep, time truncation error control dictates a maximum allowable timestep size,

Then, using our estimate for the number of iterations required for convergence as function of timestep size,

the objective is to select that target timestep size that satisfies the minimization problem,


Implicit Solvers With Embedded Timestep and Error Control

To date, reservoir simulation timestep selection strategies for error control are detached from the nonlinear solution process. Namely, there are two alternate approaches to timestep size selection for error control; a priori methods are exclusively based on extrapolation. Given state information from previous timesteps, estimates are extrapolated to constrain the next upcoming timestep size. On the other hand, a posteriori strategies will solve for a trial timestep and iterate to correct the trial timestep size until a more suitable one is attained.

Fundamental Question: Can we design implicit iterative solution methods that internally provide indications regarding time discretization errors?

Recently, a numerical Homotopty-Continuation procedure was proposed as an alternative to using Newton's method to solve implicit timesteps. In this procedure, the homotopy parameter is the solution path arc-length. Iterations in this process solve jointly for a state and a corresponding timestep size. Subsequently, and unlike Newton's method, each iterate is informative about the rate of change of the underlying physics in timestep. The mathematics of this alternate method are simple. At each implicit timestep, a nonlinear residual system of discrete equations is to be solved,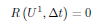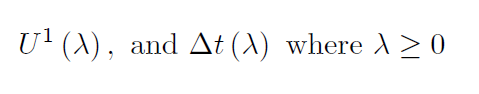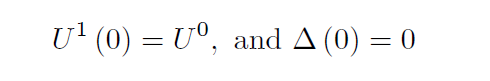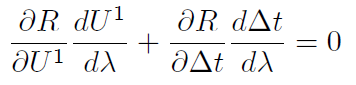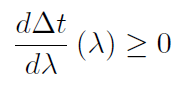
R ( U^1, \Delta t ) = 0
The method posits that for any positive timestep size, the corresponding state solution and the timestep size when augmented, form a point on a solution path. Because the solution path is a line, it may be parameterized by a single parameter such as arc-length or timestep itself,
U^1(\lambda) and \Delta t ( \lambda ) where \lambda \geq 0
and the initial point on the curve is simply the old state at the beginning of the timestep with corresponding timestep of zero,
U^1( 0 ) = U^0 and \Delta t(0) = 0
Using the chain rule to differentiate the residual system with respect to the univariate parameter yields an Ordinary Differential Equation (ODE) whose solution is the solution path itself,
J \frac{\partial U^1}{\partial \lambda} + \frac{\partial R}{\partial \Delta t}\frac{\partial \Delta t}{\partial \lambda}=0
If the homotopy parameter is chosen as the timestep size itself, no additional equations are required for closure. More generally however, an additional equation is required, ensuring that,
\frac{\partial \Delta t}{\partial \lambda} \geq 0
By numerically integrating the ODE, the solution to any timestep size may be attained. Since each successive iteration is a solution to a successively increasing timestep size, we have the hope of embedding error control directly into this process. Start from a timestep size of zero, and proceed to integrate the ODE until local time discretization errors do not exceed the given desired threshold.

Ongoing Research: Numerical integration of the ODE system
Several facets of the required numerical integration procedure are currently under study. The overriding constraint to the design of a successful continuation method for implicit timestepping is that of computational efficiency.

As with any numerical integration process, there is drift; as the numerical integration proceeds, numerical approximation errors accumulate. Subsequently, continuation strategies are typically developed using either predictor-corrector approaches and/or adaptive discretizations. We are exploring the relative merits of such alternatives. To date, we have shown that it is possible to devise strategies with computational work demands that are on par with traditional Newton methods. Continuation methods that exceed the efficiency of safeguarded Newton methods on a timestep size basis have yet to be attained.

On the other hand, when the error control is used and/or the computational efficiency over the entire duration of a simulation are studied, the efficiency of continuation methods dominates.


Nonlinear Coupling of Multiphysics

There is growing interest in the large scale simulation of coupled multiphysics. The fully-coupled approach to solving such problems leads to a coupled nonlinear system. Our current understanding of nonlinear solution methods leads to the thought that different governing forms require different asymptotic convergence behaviors. For instance, while elliptic forms are unrestricted by the propagation dynamics, owing to the global spatial support of the linearized updates, parabolic and hyperbolic forms are much more so. Our research in this direction is to devise nonlinear solution methods that exploit this knowledge. Ultimately, components that are themselves invariant to propagation speeds can be updated less frequently than components that are wave-bound. The precise relative frequency of updates will depend on the level of coupling between the sets of physics. Our approach will focus on the infinite-dimensional forms.


site stats